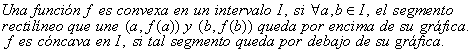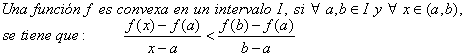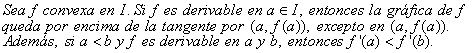Convexidad y concavidad
Aquí encontrarás los conceptos de convexidad y concavidad y los teoremas relacionados.

Definición


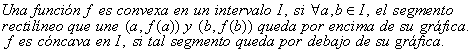
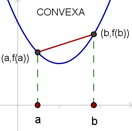
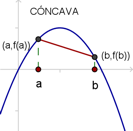
Esta condición geométrica de la definición, queda expresada de manera analítica, en el siguiente teorema.

Teorema 1

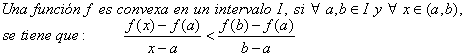
Si se invierte la desigualdad, queda definida analíticamente la concavidad.

Será de gran interés analizar la convexidad y la concavidad para funciones derivables.

Teorema 2

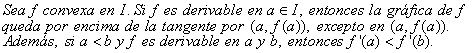
Lema


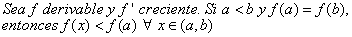
El siguiente teorema facilita saber si una función es convexa.

Teorema 3


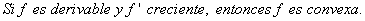
Observaciones:

1. Derivado del teorema 3, es claro que:
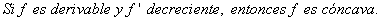
2. Un punto a, en donde una función derivable, cambia de cóncava a convexa o viceversa, se le llama punto de inflexión.
3. De manera equivalente: a es punto de inflexión de f, si la tangente a f en (a,f(a)), cruza a su gráfica.
4. Para que a sea un punto de inflexión de f, es necesario que f '' tenga signos diferentes a la izquierda y a la derecha de a. Recuerda:

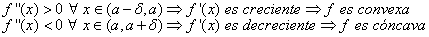
y viceversa.