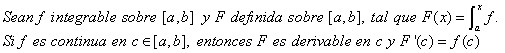
Si c=a o c=b, la derivada de F se entiende por la derecha o por la izquierda, respectivamente.
Primer Teorema Fundamental
En
este apartado, dedicado al primer teorema fundamental del cálculo infinitesimal, podrás encontrar una relación interesante entre la función integral F y la función f, en caso de que ésta sea continua. También podrás encontrar un corolario, consecuencia del primer teorema fundamental que facilita el cálculo de una integral definida, para ciertos casos.
En la demostración del siguienteTeorema se utilizará el Teorema 7 (teorema de acotación de integrales) de la sección anterior en el apartado de Álgebra de Funciones Integrables. También puedes verlo en Conceptos previos.
Teorema 1 (Primer teorema fundamental de cálculo infinitesimal)
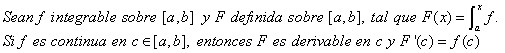
Si c=a o c=b, la derivada de F se entiende por la derecha o por la izquierda, respectivamente.
Observación
En el teorema que acabamos de ver, la función F se obtiene al variar la x, en el límite superior de la integral. Enseguida veremos el caso en que la x se encuentre en el límite inferior de la integral.
Teorema 1a (variando el límite inferior de la integral)
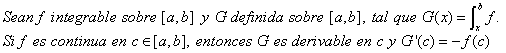
Observación
El Teorema 1a, permite además extender el Teorema 1, para el caso en que x < a. En este caso, podemos escribir:
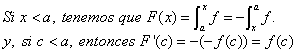
Por último, la generalización del teorema 1, es para el caso en que f sea continua en todo el intervalo [a,b].
En este caso el Teorema diría:
Teorema 1 (Generalización)
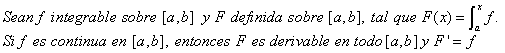
Y su demostración es igual a la del Teorema 1. Sólo es una extención a cada punto de [a,b]. Este teorema, tiene una consecuencia muy interesante como podrás ver en el siguiente
Así que para muchas funciones f continuas será fácil encontrar el valor de su integral, con sólo encontrar una función g, cuya derivada sea f. En algunos textos a éste teorema se le suele llamar el segundo teorema fundamental del cálculo. En este curso el segundo teorema teorema fundamental no exige que f sea continua, así que será un resultado un poco más fuerte, como veremos en la siguiente sección.
De lo anterior
Con sólo derivar una función g, ya podremos tener la certeza de la integral de g'. Por ejemplo, ya tenemos la certeza de que:
![]()