Área entre curvas
En
este apartado encontrarás ejemplos de cálculo de áreas entre curvas y su invariancia respecto a traslaciones. Es un apartado de mucha práctica. Trabajaremos fundamentalmente con funciones continuas. Debes tener presente el Corolario del Primer teorema fundamental, para que no te sorprendan los cálculos de integrales.
Ejemplo 1
Calcular el área ente las gráficas de las funciones
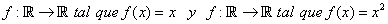
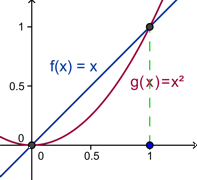
Ejemplo 2
Calcular el área ente las gráficas de las funciones
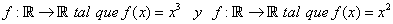
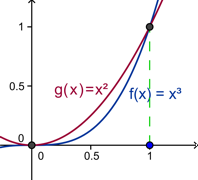
Ejemplo 3
Calcular el área ente las gráficas de las funciones
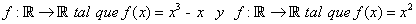
Antes de ver la solución, reflexionemos lo siguiente:
Los puntos de intersección se obtienen resolviendo la ecuación 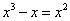 , es decir:
, es decir:
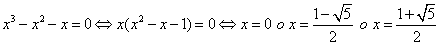
Por tanto, los intervalos a considerar son 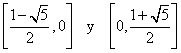 y para saber en cuál de ellos f es mayor o igual que g, o g mayor o igual que f, basta calcular un valor de f - g, en el interior de cada uno de ellos, puesto que f - g, no cambia de signo en cada uno de dichos intervalos.
y para saber en cuál de ellos f es mayor o igual que g, o g mayor o igual que f, basta calcular un valor de f - g, en el interior de cada uno de ellos, puesto que f - g, no cambia de signo en cada uno de dichos intervalos.
Así, puedes comprobar que: 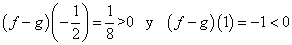 . Por tanto en el primer intervalo f es mayor o igual que g y en el segunro, g es mayor o igual que f.
. Por tanto en el primer intervalo f es mayor o igual que g y en el segunro, g es mayor o igual que f.

Un resultado (el área entre curvas, es invariante bajo traslaciones)
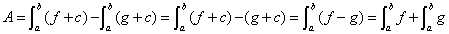


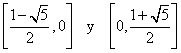 y para saber en cuál de ellos f es mayor o igual que g, o g mayor o igual que f, basta calcular un valor de f - g, en el interior de cada uno de ellos, puesto que f - g, no cambia de signo en cada uno de dichos intervalos.
y para saber en cuál de ellos f es mayor o igual que g, o g mayor o igual que f, basta calcular un valor de f - g, en el interior de cada uno de ellos, puesto que f - g, no cambia de signo en cada uno de dichos intervalos.