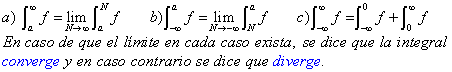
Ejemplos
Integrales impropias
En
este apartado encontrarás de funciones que no están definidas en un intervalo cerrado o bién que no están acotadas, a las que llamaremos integrales impropias en contraste con los requisitos establecidos cuando construimos el concepto de integrabilidad. ¿Recuerdas?. Pedimos que f fuese acotada sobre un intervalo cerrado [a,b].
Este apartado, lo desarrollaremos fundamentalmente con base en ejemplos, pero es necesario antes saber cómo vamos a entender este tipo de integrales y por ello, primero una
Definición 1
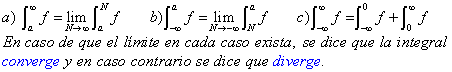
Ejemplos
Para los siguientes ejemplos se requieren previamente otros resultados. En el ejemplo 4, asumiremos que ![]() que se formaliza en una sección más adelante, pero que suponiendo algunas idéntidades trigonométricas es fácil demostrar.
que se formaliza en una sección más adelante, pero que suponiendo algunas idéntidades trigonométricas es fácil demostrar.
En los ejemplos 5 y 6 se require la igualdad ![]() demostrada en el apartado Ejercicios selectos, de la sección de Integrales y además la siguiente
demostrada en el apartado Ejercicios selectos, de la sección de Integrales y además la siguiente
Definición 2
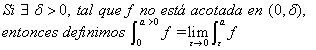
Y para los siguientes ejemplos 7 y 8, aplicaremos la definición anterior.
Algunos criterios útiles
Enseguida te presentamos algunos criterios que son muy útiles para determinar si una integral impropia es o no convergente. Estos criterior, dependen de un teorema relacionado con susceciones y su demostración la veremos en la Sección correspondiente de Sucesiones y Series, sin embargo, consideramos de gran interés presentar su utilidad en este momento.
Teorema
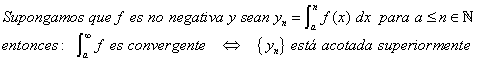
Este teorema, desencadena otros resultados, a saber:
Corolario 1
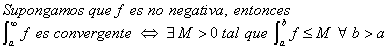
Corolario 2

Corolario 3
![]()
Otros ejemplos
En el ejemplo 9, utilizaremos los corolarios 2 y 3 y en el ejemplo 10, el Corolario 2.